기록방
구간 합 본문
💡 합의 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특한 목적의 알고리즘
🚀 합의 배열 S 정의
구간 합 알고리즘을 활용하려면 먼저 합 배열을 구해야 한다.
A[ 0 ]부터 A[ i ]까지의 합 : S[ i ] = A[ 0 ] + A[ 1 ] + A[ 2 ] + ... + A[ i-1 ] + A[ i ]

- 합 배열은 기존의 배열을 전처리한 배열
- 합 배열을 미리 구해 놓으면 기존 배열의 일정 범위의 합을 구하는 시간 복잡도가 O(N)에서 O(1)로 감소
- A[ i ] 부터 A[ j ] 까지의 배열 합을 합 배열 없이 구하는 경우, 최악은 i가 0이고 j가 N인 경우로 O(N)
- 합 배열을 이용하면 O(1)
🚀 합 배열 S를 만드는 공식
S[ i ] = S[ i-1 ] + A[ i ]
🚀 구간 합을 구하는 공식
S[ j ] - S[ i-1]
- i에서 j까지의 구간 합
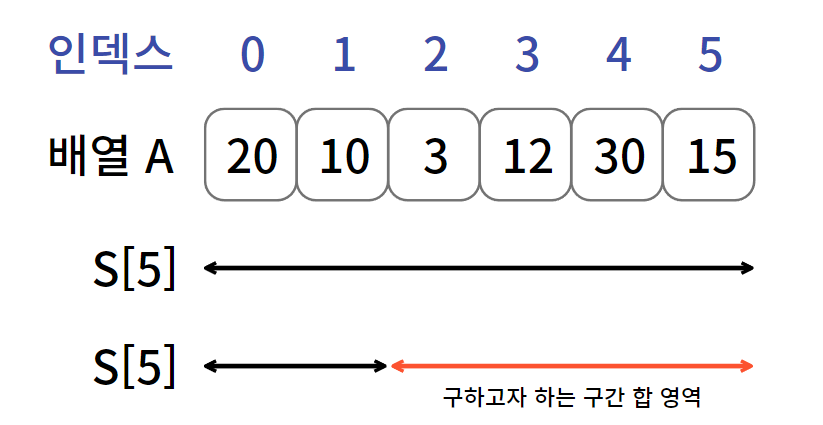
- 배열 A의 A[ 2 ] 부터 A[ 5 ]까지의 구간합
- A[ 0 ] + ... + A[ 5 ]에서 A[ 0 ] + A[ 1 ]을 빼면, 구간 합 A[ 2 ] + ... + A[ 5 ]가 나온다.
- 따라서 S[ 5 ]에서 S[ 1 ] 을 배면 구간 합을 쉽게 구할 수 있다.
🚀 A[ 2 ] ~ A[ 5 ] 구간 합을 합 배열로 구하는 과정
S[ 5 ] = A[ 0 ] + A[ 1 ] + A[ 2 ] + A[ 3 ] + A[ 4 ] + A[ 5 ]
S[ 1 ] = A[ 0 ] + A[ 1 ]
S [ 5 ] - S[ 1 ] = A[ 2 ] + A[ 3 ] + A[ 5 ] + A[ 5 ]
🚀 정리/심화
- 합 배열과 구간 합 공식을 적재적소에 활용하면 코딩 테스트에서 시간 복잡도를 줄이는 데 많은 도움이 된다.
- 1차원 배열 뿐만 아니라, 2차원 배열로도 구간 합을 구할 수 있다.
- (X1, Y1) ~ (X2, Y2) 구간의 합 : D[ X2 ][ Y2 ] - D[ X1 - 1 ][ Y2] - D[ X2 ][ Y1 - 1] + D[ X1 - 1 ][ Y1 - 1 ]
- 2차원 배열의 구간 합은 구하고자 하는 범위에서 값에 포함되지 않는 범위를 제외
- 단, 제외 할 때 중복되서 제외 된 범위는 다시 더해줌 ( +D[ X1 - 1 ][ Y1 - 1] )
- 합 배열의 원소 값을 나머지 연산해서 저장 할 수도 있다. (구간의 합이 M으로 나누어 떨어지는 i,j 쌍의 수 찾기)
- (A + B) % C 는 ((A % C) + (B % C)) % C 와 같다. 다시 말해 특정 구간 수들의 나머지 연산을 더해 나머지 연산 한 값과 이 구간 합의 나머지 연삲을 한 값은 동일하다.
- M으로 나머지 연산한 경우, 구간 합 계산에서 합 배열의 값이 같은 지점들은 그 합이 M으로 나누어 떨어진다.
- 합 배열 S를 M으로 나눈 값들로 업데이트 하고 S[ i ] = S[ j ] 라면, 원본 배열 j + 1 부터 i까지의 구간 합이 M으로 나누어 떨어진다.
- S[ i ] = S[ j ]면, (S[ i ] - S[ j ]) % M 은 0이기 때문이다.
- 간단한 알고리즘이라고 생각했는데, 심화로 갈 수록 아이디어를 착안하기 어려운 것 같다.
- 백준의 태그는 누적 합(Prefix Sum)으로 되어 있다.
728x90
'CS > 알고리즘' 카테고리의 다른 글
| 다각형 넓이 - 신발끈 공식 (Shoelace formula) (0) | 2024.03.11 |
|---|---|
| 투 포인터 (0) | 2023.06.15 |
| 시간 복잡도 (0) | 2023.06.15 |
| 그리디(Greedy; 탐욕) 알고리즘 (0) | 2023.02.17 |
| Java 코딩 테스트 교재 #4 (0) | 2022.09.29 |



