기록방
다각형 넓이 - 신발끈 공식 (Shoelace formula) 본문
신발끈 공식(Shoelace formula)은 좌표평면 상에서 다각형의 꼭짓점 좌표를 알 때 그 면적을 구하는 방법이다.
- 가우스의 면적 공식이나 사선 공식이라고도 불린다.
- 다각형의 각 꼭짓점의 좌푯값을 교차하여 곱하는 모습이 신발끈을 묶을 때와 같아 이러한 이름이 붙었다.
삼각형의 넓이를 구해보자.
세 좌표를 지나는 사각형을 그리고, 사각형 넓이에서 구하고자 하는 영역 밖의 넓이를 빼면 된다.
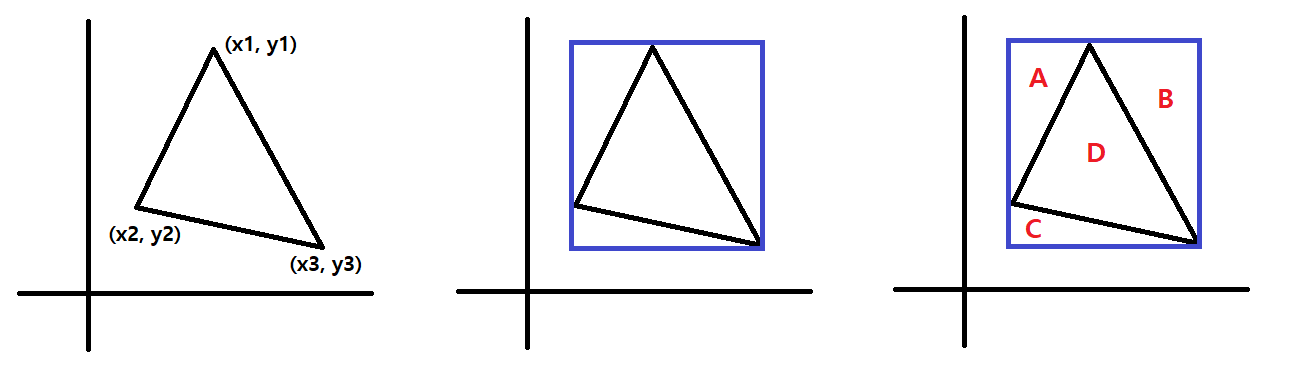
식으로 나타내면 다음과 같다.
사각형의 넓이 = ( x3 - x2 ) * ( y1 - y3 )
A = ( x1 - x2 ) * ( y1 - y2 ) / 2
B = ( x3 - x1 ) * ( y1 - y3 ) / 2
C = ( x3 - x2 ) * ( y2 - y3 ) / 2
D = (사각형의 넓이) - (A + B+ C)
여기서 D를 간단히 구하기 위해 신발끈 형태의 공식을 사용해 넓이를 계산한다.
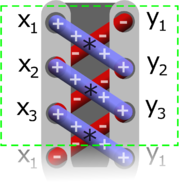
모든 좌표를 세로로 나열하고, x1은 y2와 곱해 더하고, y1은 x2와 곱해 빼는 방식으로 계산한다.
좌표를 모두 계산한 결과를 2로 놔눠 주면 구하고자 하는 삼각형의 넓이가 나온다.
신발끈 공식을 일반식으로 정리하면 다음과 같다.
다각형의 넓이 = | x1y2 + x2y3 + ... + xny1 - y1x2 - y2x3 - ... - ynx1 | / 2
마지막으로 신발끈 공식은 두 가지 한계를 갖고 있다. 이점을 유의해서 사용해야한다.
- 주어지는 좌표들은 다각형의 시계 혹은 반시계 방향으로 차례대로 주어져야 한다.
- 좌표공간에서 주어진 좌표들을 정리해 증명된 공식이기 때문에, 다각형의 시계 또는 반시계 방향으로 좌표가 주어져야 한다.
- 시계 방향은 음수, 반시계 방향은 양수가 나오기 때문에 절댓값을 씌워서 음수가 나오지 않게 한다.
- 다각형은 좌표들끼리 접촉하거나, 교차하는 선분이 없어야 한다.
- 한마디로 다각형은 ' SIMPLE POLYGON' 형태여야 한다.
- 이 외에는 볼록다각형이든 오목다각형이든 관계없이 적용시킬 수 있다.
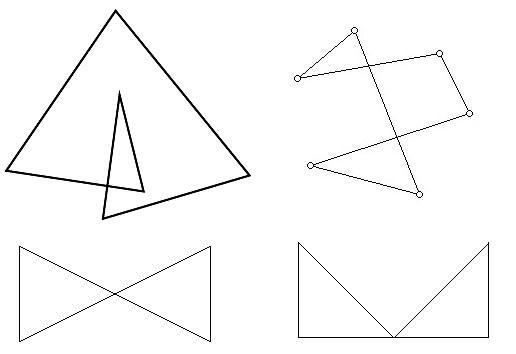
신발끈 공식으로 구할 수 없는 다각형들
[참고]
https://myengineeringworld.net/2014/06/shoelace-polygon-area-excel.html#t-1621078079560
https://ko.wikipedia.org/wiki/%EC%8B%A0%EB%B0%9C%EB%81%88_%EA%B3%B5%EC%8B%9D
728x90
'CS > 알고리즘' 카테고리의 다른 글
| 분리 집합 (Disjoint Set) 알고리즘 : Union-Find (0) | 2024.04.22 |
|---|---|
| 최장 증가 부분 수열(LIS: Longest Increasing Subsequence) 알고리즘 (0) | 2024.04.09 |
| 투 포인터 (0) | 2023.06.15 |
| 구간 합 (0) | 2023.06.15 |
| 시간 복잡도 (0) | 2023.06.15 |




