기록방
최장 증가 부분 수열(LIS: Longest Increasing Subsequence) 알고리즘 본문
최장 증가 부분 수열(LIS: Longest Increasing Subsequence)은 원소 n개의 배열의 일부 원소를 골라 만든 부분 수열 중, 각 원소가 이전 원소보다 크다는 조건을 만족하고 그 길이가 최대인 부분 수열을 말한다.
- ex) 수열 A = {10, 20, 10, 30, 20, 50} 의 경우 LIS = {10, 20, 30, 50} 이고, 길이는 4이다.
- LIS의 풀이 알고리즘은 대표적으로 DP와 이분 탐색이 있다.
DP를 활용한 LIS 구현
< 점화식 >
dp[ i ] = max( dp[ i ] , dp[ i - 1] + 1 )
dp 배열에 각 인덱스의 원소를 포함 한 LIS의 최대 길이를 저장한다.
(현재 인덱스의 앞쪽 dp 배열을 확인해 최대값 + 1. 혹은 현재 dp 배열 값 중 큰 것을 저장한다.)
- 각 dp 배열의 원소 초기값은 1이다.
- 이중 반복문을 사용하므로 O(n^2)의 시간 복잡도를 가진다.
- 구현이 간단하지만, 입력 값의 크기가 작을 경우에 사용한다.
DP LIS 핵심코드
for (int i = 0; i < n; i++) {
dp[i] = 1; // 초기값
for (int j = 0; j < i; j++) {
if (arr[j] < arr[i])
dp[i] = Math.max(dp[i], dp[j] + 1); // 점화식
}
}
이분 탐색을 활용한 LIS 구현 (1) : 길이만 구하기
LIS 형태를 유지하는 배열을 만들어, 입력 수열의 원소를 하나씩 LIS 배열에 넣는다.
이때, 넣는 위치를 이분탐색으로 찾는다.
- LIS 배열은 오름차순 정렬이 되어있기 때문에, 이분 탐색을 바로 진행할 수 있다.
- 이분 탐색의 평균 시간 복잡도는 O(logn)이므로, 총 O(nlogn)의 시간 복잡도를 가진다.
- 최종 결과로 나온 LIS 배열은 중간 원소가 수정되었으므로, 정답 배열이아니다. 따라서 LIS의 길이만 구할 수 있다.
이분탐색 LIS 핵심코드
for (int i = 1; i < N; i++) {
if (LIS[len - 1] < A[i]) { // 정답 배열 뒤에 추가
LIS[len++] = A[i];
} else if (LIS[len - 1] > A[i]) { // 들어갈 자리 이진 탐색
int mid = len / 2;
int move = mid / 2;
while (true) {
if (mid == 0) {
break;
} else if (LIS[mid - 1] < A[i] && A[i] <= LIS[mid]) {
break;
} else if (A[i] < LIS[mid]) { // 왼쪽 탐색
mid -= move;
} else { // 오른쪽 탐색
mid += move;
}
move = Math.max(1, move / 2);
}
LIS[mid] = A[i];
}
}LIS 배열은 다음과 같은 방식으로 원소를 채워 나간다.
- 입력 배열의 첫 원소 A[0]을 LIS[0]에 넣어 초기값으로 시작한다.
- A[1]부터 A[N-1] 까지 원소를 하나씩 확인해 LIS 배열을 채워 나간다.
- LIS 배열의 마지막 원소 LIS[len - 1] 보다 A[i]가 크면, LIS 배열 마지막에 바로 추가한다.
- LIS[len - 1] == A[i]는 무시한다.
- LIS[len - 1] > A[i] 라면, LIS 배열 중간 원소를 A[i]로 변경하는데, 이때 위치를 이분 탐색으로 찾는다.
- LIS의 이분탐색은 일반적인 이분탐색과 다르게 다음과 같은 조건을 만족해야 한다.
- 찾는 목표 인덱스 mid는, LIS[mid-1] < A[i] <=LIS[mid] 이다. 이때 LIS[mid]를 A[i]값으로 변경한다.
- LIS[mid-1] 을 확인하는 부분 때문에, mid가 0일때는 따로 처리해 주어야 한다.
이분 탐색을 활용한 LIS 구현 (2) : 원소도 구하기
이분 탐색을 활용한 LIS 배열의 최종 결과 원소목록을 구하기 위해서는, LIS 배열에 원소를 넣을 때 몇 번째 인덱스에 들어가는지 기록할 배열 record가 필요하다.
- 각 수가 LIS 배열에 들어갈 때 몇번째 인덱스에 들어가는지를 record라는 리스트에 저장을 한다.
- 이후에 record가 다 차면 record의 최대값으로부터 역순으로 순회하여 그 인덱스에 해당하는 값을 LIS Result에 저장한다.
- LIS Result를 오름차순으로 정렬한다.
- 실제 LIS가 완성된다.
이분탐색 LIS + record 과정
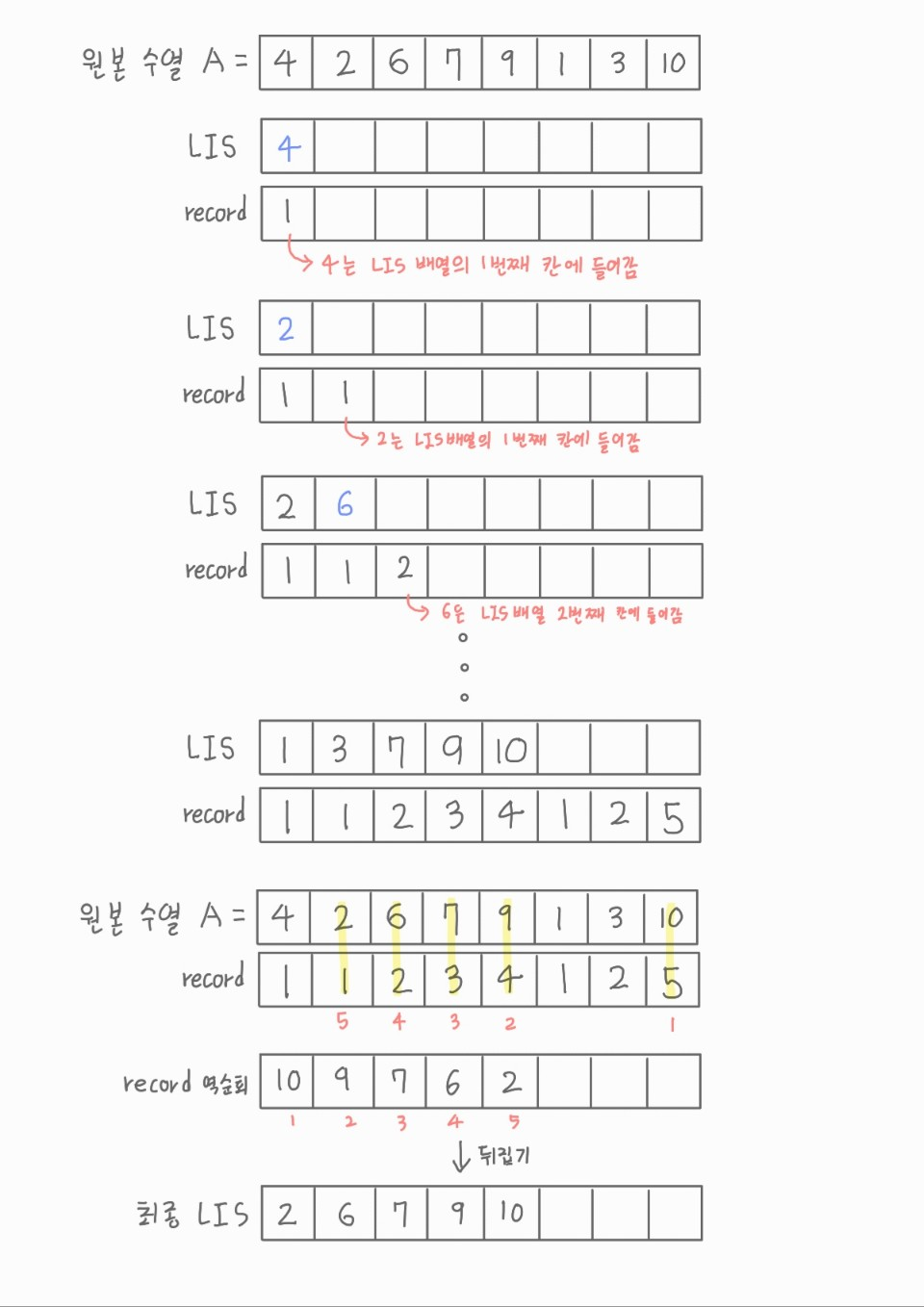
[참고]
728x90
'CS > 알고리즘' 카테고리의 다른 글
| 0-1 BFS (0-1 Breadth First Search) 알고리즘 (0) | 2024.05.10 |
|---|---|
| 분리 집합 (Disjoint Set) 알고리즘 : Union-Find (0) | 2024.04.22 |
| 다각형 넓이 - 신발끈 공식 (Shoelace formula) (0) | 2024.03.11 |
| 투 포인터 (0) | 2023.06.15 |
| 구간 합 (0) | 2023.06.15 |



